EL PROBLEMA DE LAS PUERTAS
Este curioso problema, también conocido como el
problema de Monty Hall, está inspirado en el concurso estadounidense emitido
por televisión desde 1963 al 1990, llamado Let’s make a deal (hagamos
un trato) y le pusieron el nombre de Monty Hall en honor a su
presentador.
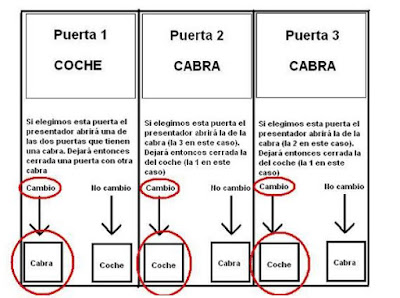
Supongamos que nos encontramos en un concurso parecido
a “Let’s make a deal” y nos ofrecen tres puertas, en dos de ellas hay cabras y
en la otra un precioso coche. El presentador, que ya sabe lo que hay detrás de
cada puerta, nos dice que escojamos una de ellas y nos decidimos por la
tercera. Para dar más emoción al asunto el presentador abre la segunda y vemos
que detrás hay una cabra. Para finalizar el presentador nos ofrece la
posibilidad de cambiar la tercera puerta por la primera. ¿Qué es mejor,
quedarnos con la tercera, aceptar la propuesta del presentador o da igual lo
que escojamos ya que hay las mismas probabilidades de que el premio este en una
o en otra?
Muchos de nosotros pensaríamos que la tercera opción
es la correcta, que da igual cual escojamos ya que hay 50% de probabilidades de
que este en una o en otra, pero esto no es cierto y ahora veremos por qué.
Si escogemos la opción de no cambiar de puerta la situación
se nos presenta de la siguiente manera:
El presentador nos hace escoger puerta dándonos cuenta
de que tenemos 1/3 de probabilidades (33%) de escoger el coche y 2/3 de
probabilidades (66%) de escoger las cabras. Escogemos la tercera y el
presentador nos abre la segunda y vemos que hay una de las dos cabras. Como
hemos escogido no cambiar nos quedamos con los mismos porcentajes que al
principio un 33% de conseguir el coche y un 66% la cabra. Esto no es nada
bueno.
Veamos qué ocurre si aceptamos la propuesta del
presentador y decidimos cambiar de puerta:
El presentador nos dice que escojamos puerta y como
hemos dicho antes hay un 66% frente a un 33% de escoger las cabras, escogemos
la tercera e igual que antes el presentador abre la segunda y hay una cabra. Es
decir ya solo hay una cabra y un coche. Si cambiamos a la primera las
probabilidades cambian completamente y ahora tenemos un 66% de conseguir un
coche frente al 33% de las cabras.
El porqué, es muy sencillo, el presentador siempre abrirá
la puerta que no hayamos escogido donde habrá una cabra. Si al principio la
puerta que hemos escogido tiene una cabra al cambiar de puerta nos llevaríamos
el coche, no obstante, si la primera puerta que escogemos contiene el coche al
cambiar de puerta nos llevaríamos la cabra. Pero como hemos dicho antes hay un
66% de escoger una cabra al principio, por lo tanto hay un 66% de llevarse el
coche.